The Hopkinson scale (or cubic or Hopkinson-Cranz) equation can be used to work out how the mass of explosive changes with distance, so that the same peak pressure is applied at a target zone.
(In this, pressure will be used to mean overpressure or side pressure, which is generated by the denotation of the explosive.)
From Hyde (1965), the Hopkinson scale equation is given as:
To calculate the pressure of an explosion at a target zone Hyde (1965)
gives the following:
Now I don't fully believe this equation, but I don't work out the pressure; I just model with empirical data sets. Other equations are available in Bulson (1997) [really good book, must read if interested in this field], and Baker (1983) [good if you have sleeping problems].
Now how to you design for this? This leads to optimisation for blast tolerant structures, which I will not address here, but possibly some other time if people are interested. The best way to do this is give the example that I am researching. This is based on a paper I should be presenting at IMPLAST 2000 in Melbourne, Australia and an internal report for AME CRC (Australian Maritime Engineering Cooperative Research Centre).
Firstly, what do we want to do?
Or what are the operational requirements of the transverse bulkheads?
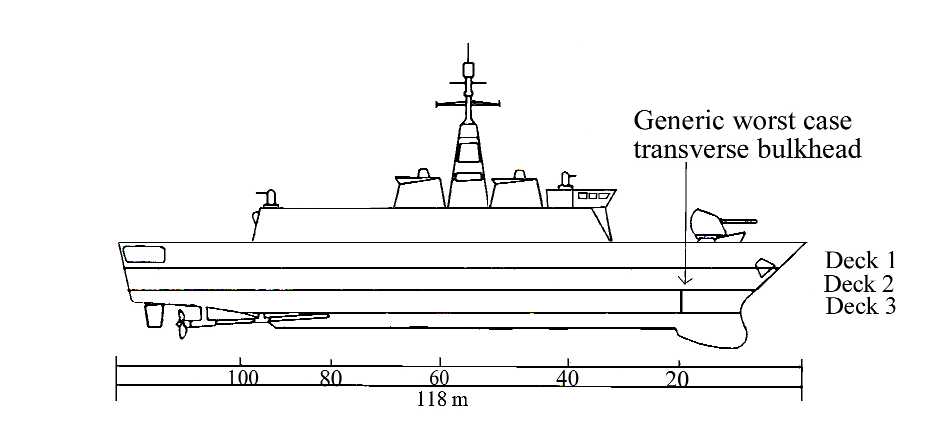
The operational requirements will be based around the capabilities that a transverse bulkhead on deck 3 at 19.2 m from the bow on a vessel 118 m long moving at 30 knots, see Figure 1, should be able to be fulfil. This is potentially the worst position for a transverse bulkhead due to the following reasons
- the depth of the bulkhead would mean the pressure head due to a tank or flooding load would be at its highest,
- this distance forward means that the dynamic factor from the ship motion, including slamming, would be significant
- the vessel would be wide enough to have all the capabilities and requirements that are under consideration in this design criteria for a transverse bulkhead. Principally, at this distance from the bow, this vessel is wide enough for housing heavy equipment and the bow is unlikely to separate due to the air-blast load.
In the design of structures you have to consider all load situations. For this case, there are three separate loads situations
- Pre-air-blast loads
- Air-blast load
- Post-air-blast load
The first load considered is the hydrostatic load due to a tank. This hydrostatic load is solved by the method given in BV104 (1982). In this case the value of the hydrostatic pressure due to a tank is 90 kPa.
The second load is the structural load, which come from Chalmers (1993), where for the sides of the bulkhead it is 93.15 MPa and for the top it is 22.5 MPa.
In the analysis of these combined loads it is required that the solution stay within the elastic regime. A J-integral procedure will be used to confirm that no rupture occurs.
The air-blast load against the naval transverse bulkhead will be assumed to be 150 kg of TNT equivalent explosive at 8 m. This load is comparable with the critical blast load considered by most western navies in the design of new vessels, Reese et. al. (1998) and OPNAV (1988). Although this is a low-ish air-blast load compared to these papers.
The response of the transverse bulkhead to this blast load will be critical in two respects. Firstly, as with the pre-air-blast loads, no rupture is permitted within the transverse bulkhead structure. Secondly, a maximum permanent deformation of the transverse bulkhead will be set. This is due to pipes penetrating through the bulkhead, equipment and walkways close to the bulkhead, and that a post-air-blast load being supported by the bulkhead.
An air-blast load of a 150 kg TNT equivalent explosive at 8 m inside a vessel is equivalent to, by the Hopkinson scale method, 7 kg of Comp-B at 3 m. The data used comes from two separate sensors positioned at 550 mm and 1150 mm radially from the centre of the bulkhead. Additionally, in steel, an elastic stress wave will travel between these two points in approximately 0.12 msec. Conversely, the time between the blast wave reaching the 550 mm pressure gauge and the 1150 mm gauge is approximately 0.5 msec in air. This can be used to tune the air-blast load to be more dynamic in nature.
The blast pressure profiles both start at zero pressure and end at zero pressure and last 5 msec, which can be assumed to be less than the period of the 1st natural harmonic of a transverse bulkhead.
The maximum permanent deformation that can be accepted by a naval transverse bulkhead is 100 mm. This maximum deformation was established due to pipes penetrating though the bulkhead as well as equipment and narrow walkways that may be near the bulkhead.
In regards to fulfilling the requirement that no rupture occurs, a J-integral procedure is also required.
The post-air-blast load is flooding of the compartment after an explosion has occurred.
The flooding load comes out to be 52 kPa.
The deformed transverse bulkhead, due to the air-blast load, is permitted to deflect a further 5 mm due to the flooding load. The J-integral procedure will be used here to test for rupture.
In relation to the structural load, it is assumed that structural redundancy within the vessel will absorb it.
(Some interesting assumptions in that statement about structural redundancy, but could lose a finger or two trying to explain them.)
I wont go into this, unless asked, but this is a very interesting way of testing for rupture. Gets some what mathematical but fun. As a side note to my knowledge no one else has tried to use this method.
Test, fem and scale models
In my research I am finite element modelling using data from semi-full size tests. This is the best way to do this type of stuff, as scale model tests do not really work. The reason why scale model tests do not work is quite simple. Take a scale model test that works, i.e., a static load is applied to some steel in the elastic realm. Now if you scale this down by say a factor of λ. Then the thickness, dimension and load can all be scaled down by λ. Now take the explosion situation where the structure does not have a static load and acts elastic-plastic. In this case you have the steel stretching so the scale factor is λ2 and fracture of the steel so a scale factor of λ3. So how much explosive should be used? What scale factor should be applied to the thickness and dimensions? No one really has a clue about these questions. I would guest in the situation of the 1/8 scale structural test that their used 1/10 of explosive power under consideration. But that is gut feeling only.
Other scaling problems can relate to forces and such things that cannot be scaled, i.e., gravity.
There are good non-linear dynamic finite element packages available that with good empirical data will give you very good results, i.e., I get better than 10% on my PC.
Chalmers (1993) and others state that thermal loads from an explosion need only to be considered for aluminium and composite super structures subjected to a nuclear blast criteria. This is outside my area but, in the situation of a nuclear weapon detonation close to nuclear missile silo, you will have a thermal load. The thermal load will weaken a structure, by melting or softening it, and additionally make the structure more brittle. Brittleness comes from re-solidification of the materials. Like seen in welding with the heat-affected zones.
Well, that's it.
- Baker, W.E., "Explosive hazards and evaluation", Elsevier Scientific Pub. Co., 1983
- BV 104-1 "Structural analysis of the ship's hull (strength specification)", July 1982
- Bulson, P.S., "Explosive loading of engineering structure: A history of research and a review of recent developments", E and FN Spon, 1997
- Chalmers, D.W., Ministry of defence — design of ship's structures, HMSO, 1993
- Those in the business know what this is, the others it is a good read.
- Duffey, T.A., "Dynamic rupture of shells", Structural Failure, Ed. T. Wierzicki and N. Jones, John Wiley and Sons, New York, U.S.A., 1989, pp. 161 — 192
- Jones, N., "Recent studies on the response of structures subjected to large impact loads", Ship Structures Symposium '93, SNAME and SSC, 1993, pp. C-1 — C-22
- D. Karagiozova and N. Jones, "Some Observations on the Dynamic Elastic-Plastic Buckling of a Structural Model", Int. J. Impact Engng, 16, No. 4, 1995, pp. 621-635.
- N. Jones, "Structural Impact for Marine Structures", Advances in Marine Structures 2, 1991, 2, pp. 251-275.
- N. Jones, "Recent Studies on the Dynamic Plastic Behavior of Structures", Applied Mechanical Review, ASME, 42, No. 4, April 1989, pp. 95-115.
- Ghose, D.J. and N.S. Nappi, "Re-examination of design criteria for stiffened plate panels", SSC-382, 1994
- Hyde, D.W., "Fundamentals of protective design for conventional weapons", TM 5-855-1, Structural Laboratory, Waterways Experimental Station, For the Department of the Army, US Army Corps of Engineers
- OPNAV Instruction 9070.1, USN, Ser 09/8U501139, Chief of Naval Operations, Washington, 1988
- Reese, R.M., Calvano, C. N., and Hopkins, T.M. "Operationally-Oriented Vulnerability Requirements in the Ship Design Process", Naval Engineers Journal, January, 1988, pp. 19-34
- Williams, M., "A structured approach to warship design", Navtec'90, International Conference on Interaction Between Naval Weapons Systems and Warship Design, RINA, 1990.
- 26 November 1999
- Updated